it is possible to evaluate presidential forecasts in less than millennia

get creative; don't be a nihilist

This blog post is now a preprint with errors corrected, please refer there for the latest version of my argument.

This week, a curious article was published in Politico saying don’t trust presidential forecasts because it would take “decades to millennia” to evaluate them. The Politico piece was essentially the press release for a new academic paper by Justin Grimmer, Dean Knox, and Sean J Westwood (henceforth GKW). These are highly decorated political scientists, and I like other work by all three of them. But this paper, as the kids say, ain’t it.

The basic idea is that since presidential elections are rare, and state-level outcomes within a single presidential election are highly correlated, we need a lot of presidential elections to figure out which forecasts are good or bad. On its face, this idea is not crazy. Presidentials only happen every four years, and if you think you need a hundred observations to tell two forecasters apart, and that’s 400 years. But when you think about it more, this idea is wrong. There are in fact at least three ways to evaluate political forecasts that provide information on if the forecaster is good or not on shorter time spans.

Adding to the issues with this paper, the motivating idea behind this paper is strange: GKW think probabilistic forecasts are harmful because the public misinterprets them which causes them to avoid voting

Even under the most optimistic assumptions, we are far from being able to rigorously assess probabilistic forecasters’ claims of superiority to conventional punditry. Yet despite the lack of demonstrable benefits, forecasts induce known harms: producing vacuous, unverifiable horse-race coverage; potentially depressing votes for forecasted winners; and misleading the public and campaigns alike. Taken together, it is hard to justify the place of forecasts in the political discourse around elections without fundamentally recalibrating claims to match the available empirical evidence.

So we’re really not exploring if forecasts or good or bad, we need to say that forecasts are bad to advance this secondary agenda of not wanting them displayed prominently because they have other harms. Not a great argument.

If GKW’s argument was: “Forecasts may inform us, but they have harms that outweigh that information,” I could potentially get on board with that. I am not intimately acquainted with the evidence on forecasts depressing turnout but I know it exists and that the authors of this paper buy it, so perhaps there is something there.

But that is not the paper GKW wrote: they wrote a paper saying basically that it takes so long to figure out if forecasts provide information that they are no better than “conventional punditry” (or at least if they are better it is impossible to know). I think this idea is wrong, and that the authors have unfortunately made a very bad argument (forecasts are bullshit) in service of a potentially plausible one (forecasts may depress turnout).

I’m going to detail the authors’ statistical argument here, and I’m going to provide some strategies for thinking about forecasts that can plausibly let us evaluate them on shorter time spans than decades-to-millennia. GKW honestly should have considered some or all of these themselves, and their lack of doing so makes me think they just wanted to make the normative argument that forecasts are bad rather than doing honest science.

This is a blog post, there may be mistakes. I encourage you to read my code (there’s not much of it) and call me out if you see errors. I also welcome discussion in the comments or on Twitter.

Strategy 0: Just use Bayes’ theorem

EDIT NOTE: I messed up the denominator of Bayes’ theorem in my first version and have corrected it 🤠

The position taken by GKW is that single elections give little information. This is wrong. Let’s use Bayes’ theorem to show this, along with a famous example from 2016. In 2016, Sam Wang of the Princeton Election Consortium put for a meta margin model which gave Hillary Clinton a 93% chance to win on election day, while Nate Silver’s model gave Hillary a 71% chance to win. We know that Donald Trump did win.

Let’s say we had a high opinion of both of these poll aggregators before hand, and we thought that they had an 80% chance to be right. Let’s say we think American politics is closely divided and we assume both Hillary and Trump had a 50-50 shot of winning going into the campaign, so if the forecast is wrong we will give him a 50-50 chance.

We can then use Bayes’ theorem like so to get a posterior probability of them being right given their prediction probabilities.

• P(forecast correct | Trump wins) = P(Trump wins | forecast) P(forecast) / P(Trump)

For Sam Wang, this comes out to

• 36% = 7% * 80% / (80% * 7% + 20% * 50%)

And for Nate Silver this comes out to

• 70% = 29% * 80% / (80% * 29% + 20% * 50%)

So we can see even from this single event that, given a few assumptions, we believe that Nate Silver was roughly twice as likely to have a correct forecast as Sam Wang. We go from thinking Sam Wang is right 80% of the time to just 36%! It turns out that because probabilities contain a lot of information you can learn a lot from a single event.

This strategy is generally useful for weeding out highly confident wrong forecasts.

Strategy 1: A better simulation

The authors’ model of the world (p 24, section A.2 of their paper) relies on detecting calibration differences for a single election with p(win for candidate 1) = 89%. They repeat this single election and ask “how long until an oracle forecaster achieves better performance than an inferior one.” I think this simulation has some value, but it answers a somewhat different question than the authors think. GKW premise their paper on forecasts having little value, which means you want to compare a forecast to random guessing (or perhaps a replacement-level pundit), not to a second-best alternative. Another way to say this is GWK think they are answering “how do we figure out which forecasts are good” but they actually answer “how do we figure out which forecast is the best.”

If you want to figure out if one of two forecasts are the best, and they are both very good, it may take a long time. In that realm, GKW is correct. But this is not the argument they make in words in their paper. But if you want to figure out which forecast is better than random guessing, the situation is very different and you need to conduct a different simulation.

Let’s do a little alternate simulation here: assume that one forecaster guesses randomly, providing a win probability in (0,1). Another forecaster provides a real forecast where we can vary the forecast quality. We want to plot ability to distinguish forecasts from random guessing in two dimensions: by forecast goodness and by number of elections. This will give us an idea if, even compared to a random baseline, we can detect good forecasters in a short number of presidential election cycles. If we can, this means that even if two forecasts are hard to distinguish from one another, if we can say they provide information GKW’s main argument is wrong.

There’s a wrinkle, though, you can come up with a lot of ways to generate a number between 0 and 1 because the beta distribution is pretty flexible. So I tried two parameterizations for our hypothetical forecaster: a concentration parameter of 5 and one of 0.7. These correspond to the following distribution shapes. The first one is more reasonable and the second one is more extreme. Obviously in the real world there is some optimum that people have thought very hard about, but these will do fine for now.

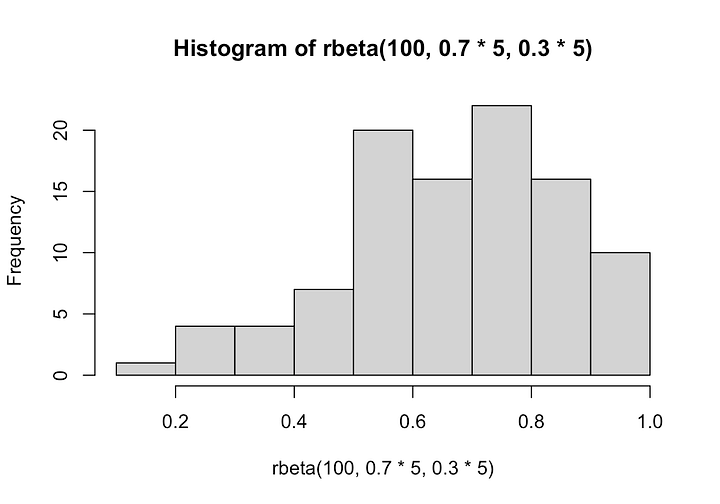
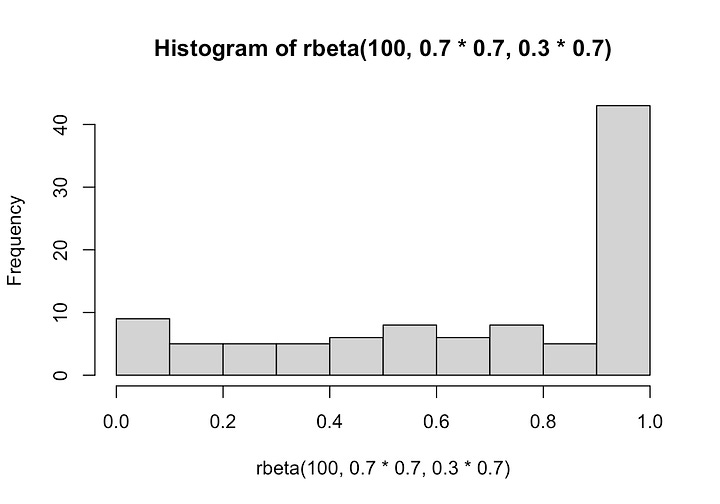
Doing this simulation (which you can replicate here), we see that in the case (left plot) where forecasters don’t concentrate their probabilities too close to zero and we compare to random guessing, we start to see traditional stat sig on average around 7 to 10 elections for good forecasters. If the forecaster is extremely good, with 90% accuracy, you’ll see traditional stat sig on average with just 3 elections compared to random guessing. These are t-value averages from 1000 simulations.

So even if we simply evaluate forecasts probabilistically using the most basic methods, we can convince ourselves that, even given the GKW’s strong assumption that presidential elections are unicorns not comparable to anything else, we can evaluate forecasts relative to random guessing if the forecasters are decent-to-good.

Of course, if forecasters do dumb things like get overconfident (right plot) it may take awhile. But the competitive landscape of forecasters should address this by weeding out bad assumptions.

Strategy 2: Elections are like other elections

Having established that there are scenarios where a relatively small number of elections can separate good forecasts from junk, I’m now going to argue that we can increase the number of “elections” in two ways: first by combining presidential forecasts with other political forecasts, and second by examining plausibly uncorrelated microdata (such as demographic groups).

GKW take the strong position that presidential elections are unicorns that cannot even be compared to other elections in the United States such as midterms. In Grimmer’s words, they are “distinctive.”

I don’t believe this. Rather, I believe that if someone is good at forecasting a presidential, they are probably good at forecasting a midterm and vice versa.

If you simply accept that midterms and presidentials both go in the analysis, you’ve doubled the number of elections you’re considering. So now we’re hitting 10 cycles in 20 years rather than 40, and so on.

Now, what about forecasting off-cycle governor elections? Specials? State houses? And so on.

The number of American elections is fairly large, even if you insist that all elections held on a particular day can be treated as only a single observation with no more fine-grained analysis providing additional info. Further, specials and off-year governor elections are plausibly *harder* than forecasting a presidential. The presidential has tons and tons of data. The 2021 Virginia Governor’s race? Much less data!

So you can really move up the “number of elections” ladder pretty quickly if you insist on forecasting all elections (as professionals do!).

Strategy 3: Demographic groups and other microdata

While it is true that state-level results are highly correlated with one another (so you don’t have 50 independent observations from 50 states), they are not perfectly correlated! And this increases the number of “effective elections”. Using the Economist’s state level correlation matrix from last cycle and a formula chat GPT gave me (see the R), I get the number of 5, meaning that the 50 states provide the equivalent of 5 independent observations. So now every presidential counts for 5 observations, again moving us up the number-of-elections scale.

To go deeper and get more hand-wavy, if you look at voting patterns among, say, midwestern non-college whites and young female Hispanics in Nevada, it’s more plausible to think groups are less correlated. If we must produce forecasts that provide geo-by-demo-by-other-demo forecasts, the number of effective observations goes up even more. Again, real forecasters produce forecasts with ever-increasing specificity that we can evaluate.

All of our major forecasts are probably pretty good

In GKW’s framework, we are comparing like 538’s forecast to the Economist’s. I think this is the wrong question to ask when determining whether forecasts are useful at all. The core argument made in the paper is that forecasts writ large are not useful, not that like the Economist’s forecast is better than 538.

If you want to compare two good forecasts, it may take you a long time. But if you want to compare a major forecast to the alternative of vibes, it is easy to see that these forecasts provide information over the vibes.

It is entirely possible that all major forecasts are quite good, because the only ones that have survived in the marketplace are quite good. Remember when Rachel Bitecoefer hired a chemistry grad student to model the 2020 election using independent coin flips for each state? Well, there’s a reason that model is no longer around: because it got made fun of so aggressively on Twitter for being obviously wrong that it was taken down within a week.

Whether the forecasts are more accurate than a replacement-level pundit is still a hard question to answer, because the replacement-level pundit might be quite good. But that’s also endogenous because of the rise of good forecasts. This is presumably a thing that GKW could try to measure, but they don’t.

My belief here is that a pundit is like 6/10 and a forecast model is like 8/10 on a totally arbitrary 10 point scale I just made up. But I’ll leave that for political scientists to do more research on.